Regression Analysis is (relatively) easy
Hypothesis: Using only a subset of GC metrics we can compute linear regression functions using only heap space used to predict when the next GC occurs. To do this we don’t need access to all the metrics per host, just a subset. And we can extend it in the future to use multiple variables and/or regression classification to predict which GCs are likely to be “long”.
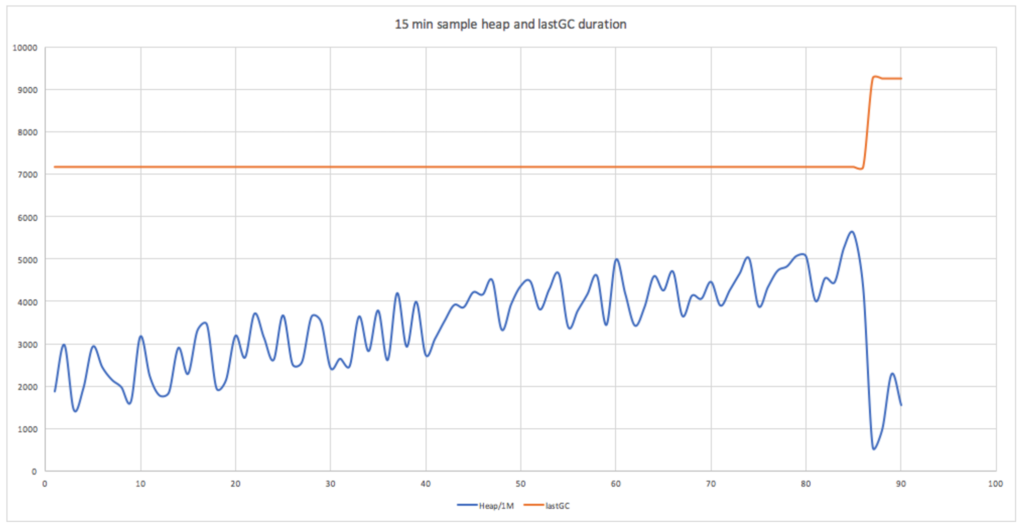
Let’s look at some sample heap space data and GC time information. Here’s a graph showing heap space used increasing over time (x-axis, seconds) and then a GC kicking in (orange line), resulting in a reduction in the heap space used. The GC value is the duration of the last GC so changes from approximately 7s to 9s.
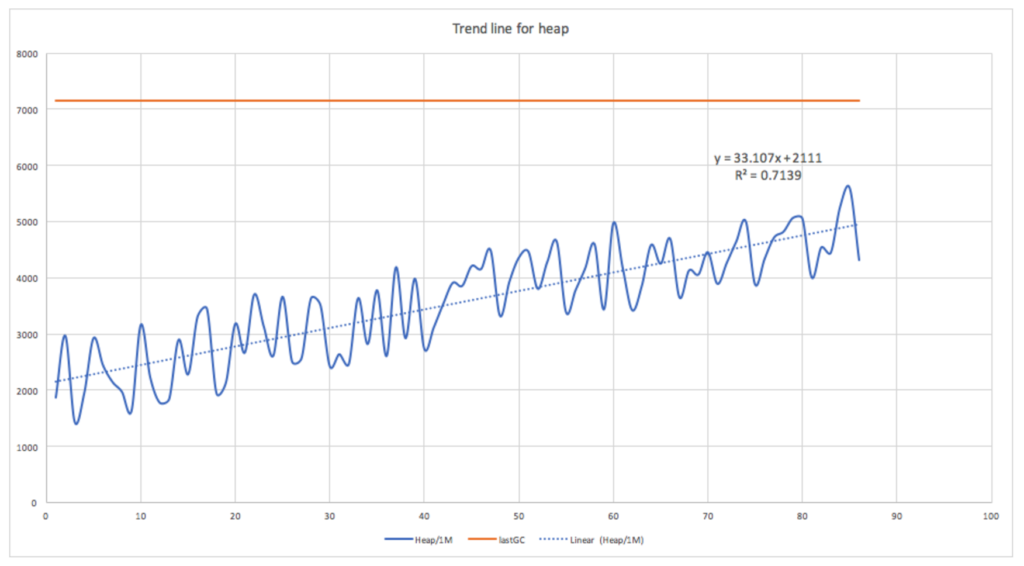
The following graph shows a linear regression function fitted to the portion of the heap space used graph in the interval between GCs. It shows a significant linear correlation with R- squared 0.71.
Is this useful? Assuming we know (or can compute) the amount of heap used that triggers a GC then yes. This may be node-specific (depending on how much heap is available), may change (as more memory is allocated), and may be a percentage (which we have to compute, for this example it was 70%). Obviously, the slope of the function will vary across and even within nodes depending on the frequency of GC (which may depend on many other variables which we’ll look at next time), so the function needs to be computed for each node for each interval between GCs. This requires us to do a few things: Find when each GC occurs so we can determine the time period from the end of the last GC to the start of the next GC to use as the sample period to compute the regression function over; for each interval normalise the actual timestamps to relative time (in seconds) from the start of the interval; keep track of the amount of heap used that triggers the GC (or compute the percentage used); and find sufficient samples for a node to make predictions and check the accuracy and usefulness of the results.
Some preliminary inspection of sample data showed a few problems. Using GC startTime and endTime seemed to be the obvious way of finding when GCs occurred. However, there was something odd about the times as they were in the distant past, in fact, they were about 300 times less than expected. Oh, that five minutes isn’t it. Turns out that they had been truncated to bucket_time making them useless for my purpose. Another thing to watch for with Cassandra timestamps is that they are in UTC. If you convert them to a Java Date type they will be in local time. The Java Instant class is a better representation once you read the timestamps on the client side (Instant is UTC, and has lots of useful time comparison methods).
Is there a way of using either GC duration and/or collectionCount to compute the GC start/end times? Yes, in theory. Both approaches worked ok, but I noticed large gaps in the timestamps for most nodes which made using duration tricky. The final version used collectionCount and discarded GC events that were more than 1 count different. But why were there gaps in the data?
Materialization accidents—“beam me down Scotty!”
My suspicion turned to the materialized views (MVs) I had to created to make the queries easier. Obviously, MVs take time to populate from an existing table, but how do you know if they are complete? There are two system tables to check, one shows build in progress, and one shows built views completed (system.built_views):
keyspace_name | view_name | generation_number | last_token
———————-+————————-+—————————-+—————————–
instametrics | host_service_time | 16563 | -9178511905308517795
instametrics | host_service_value | 16563 | -9178511746231999096
So this probably explained the data gaps – a few days after creation the MVs were still being built. In fact, I suspect they have got “stuck” (anyone know how to unstick them? I tried dropping a MV and trying to create another but this resulted in other nasty things). Given its sci-fi origins, I should have been wary of Cassandra Materialization! The Star Trek Transporter was notoriously accident-prone often resulting in duplicates, combined life forms, being turned inside out, or just plain non-existence, whoops. Worst Star Trek Transporter accidents!
I finally got the code working and ran it on a subset of 100 nodes. However, it was only finding a relatively small number of GCs per node due to the data gaps. I realized that the default read consistency level is only one, which means that only data from the first node it is found on is returned. I tried increasing the consistency level (to QUORUM) which resulted in more GCs found. See code on GIST:
Each regression analysis uses only the first half of the available data, and if the R-squared value is over 0.5 then the computed function is used to predict the next GC time, and the percentage error is computed and averaged over all results founds and reported as follows:
Total time = 428,469ms
avgPerErr = 21.59 gcAvgInterval = 13,447.88s used 42.0 out of 218.0
The analysis took 428 seconds, for the regressions that had a sufficiently high correlation (about 20%), the average percentage prediction error for the time of the next GC was 22%. The average time between GCs was 13,447 seconds, so the average error is about 3,000 seconds. So this approach would work well, but for only 20% of cases. There’s obviously something more complicated going on for the majority of cases requiring us to get even closer to the monolith, we need to install the analysis code closer to the data.