Massively Scalable Geospatial Anomaly Detection with Apache Kafka and Cassandra
In this blog we discover that we’ve been trapped in Flatland, and encounter a Dimension of the Third Kind. We introduce 3D geohashes, see how far up (and down) we can go (geostationary satellite orbits, the moon, and beyond), revisit Cassandra partition sizes, and come back down to earth with a suggested 3D geohash powered hazard proximity anomaly detector application for Drones!
1. What Goes Up…
As if changing from believing that the earth is “flat” to round isn’t hard enough for some people, there’s also the challenge of moving from 2D to 3D!
“Either this is madness or it is Hell.” “It is neither,” calmly replied the voice of the Sphere, “it is Knowledge; it is Three Dimensions: open your eye once again and try to look steadily.”
― Edwin A. Abbott, Flatland: A Romance of Many Dimensions
In the world of Flatland there are only 2 dimensions, and the Sphere (who inhabits 3D Spaceland) tries to explain height to the 2D creatures than inhabit it!
So let’s try and imagine a 3D world, so we can go Up:
( (Source: Wikipedia)
(Source: Wikipedia)
…And Down!
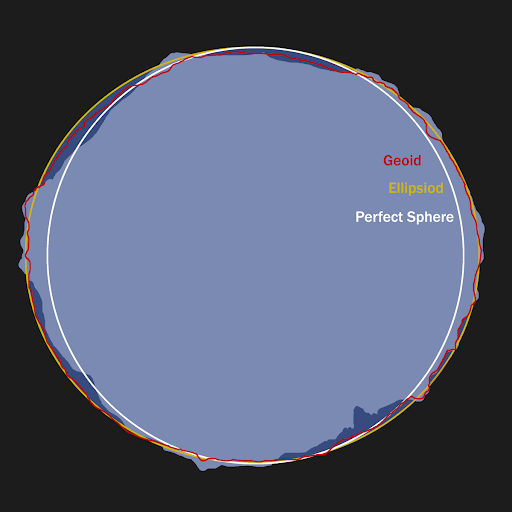
It’s a big jump from a flatworld (e.g. a 2D map) to even just a surface on a round ball (i.e. a sphere). But introducing a 3rd, vertical, dimension has more challenges. Where do you measure elevation from? The centre of the earth? The surface of the earth? And guess what, the earth isn’t actual spherical (white line), it’s an ellipsoid (orange line), and even has dips and bumps (geoid height, red line). This diagram shows the vertical complications of a (cross section of a) real planet:
Does the vertical dimension matter? Well, there are actually lots of things below the nominal surface of the earth. For example, the deepest borehole, the Kola Superdeep Borehole, has a depth of 12,226m (as the top of the hole proclaims):
It’s 11km to the bottom of the sea – the deepest dive ever was made recently to 10,928 m down in the Mariana Trench, 16m deeper than the previous record set way back in 1960, finding a plastic bag and a few weird fish:
 An Arrowtooth Eel swims at the bottom of the Mariana Trench. (Source: New York Post)
An Arrowtooth Eel swims at the bottom of the Mariana Trench. (Source: New York Post)
By comparison, it’s only 4km down the deepest mine, 2.2km down the deepest cave, and the Dead Sea is 400m below sea level.
 (Source: Shutterstock)
(Source: Shutterstock)
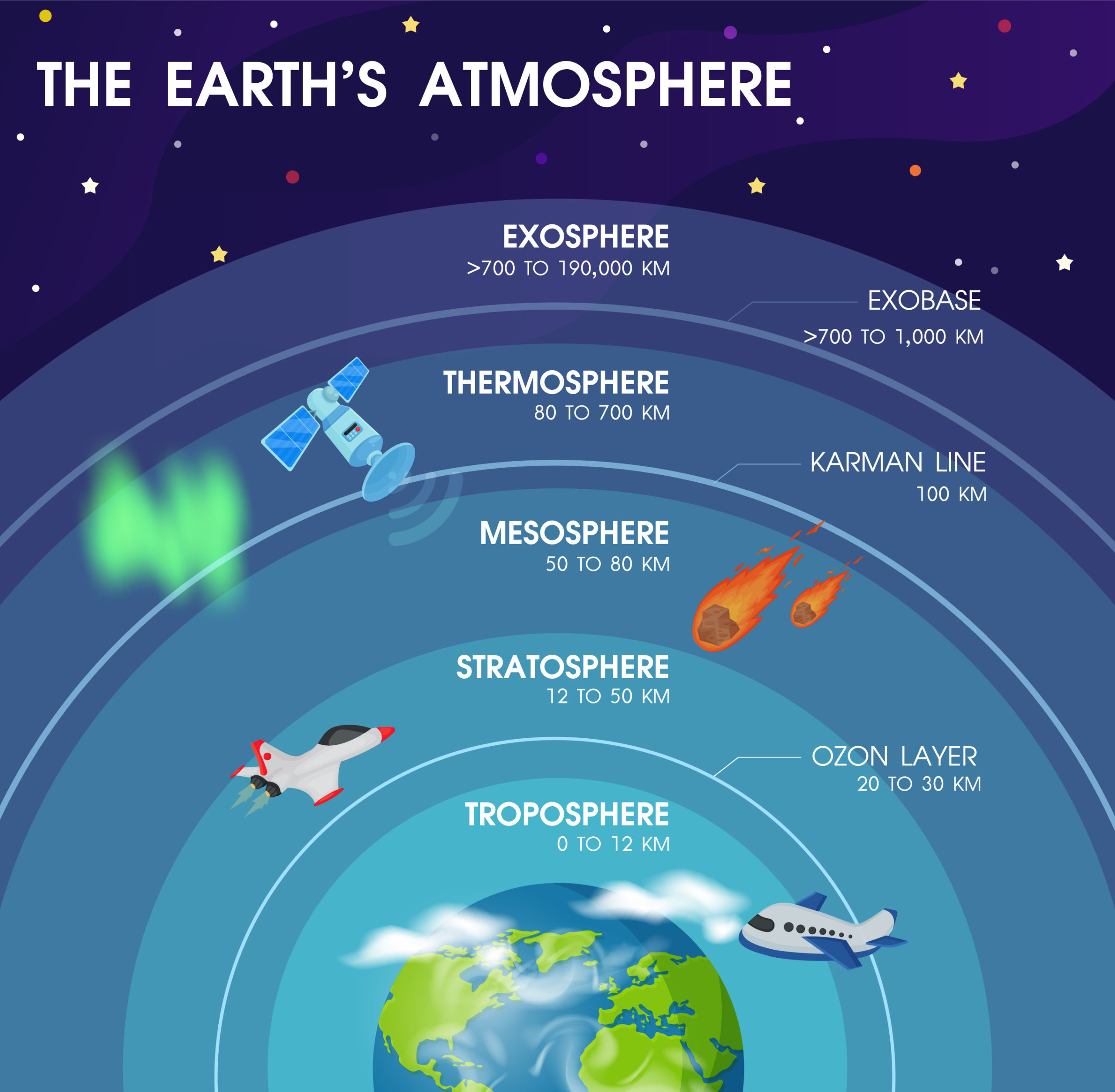
Going in the other direction, altitude above the earth can range over essentially infinite distances (the galaxy is big), but coming back closer to earth there are some more useful altitudes. Planes and some drones operate up to 10km up, jet planes up to 37km, balloons up to 40km, and rocket planes up to 112km!
 (Source: Shutterstock)
(Source: Shutterstock)
Further out, the orbits of satellites can extend more than 30,000 km above sea level:
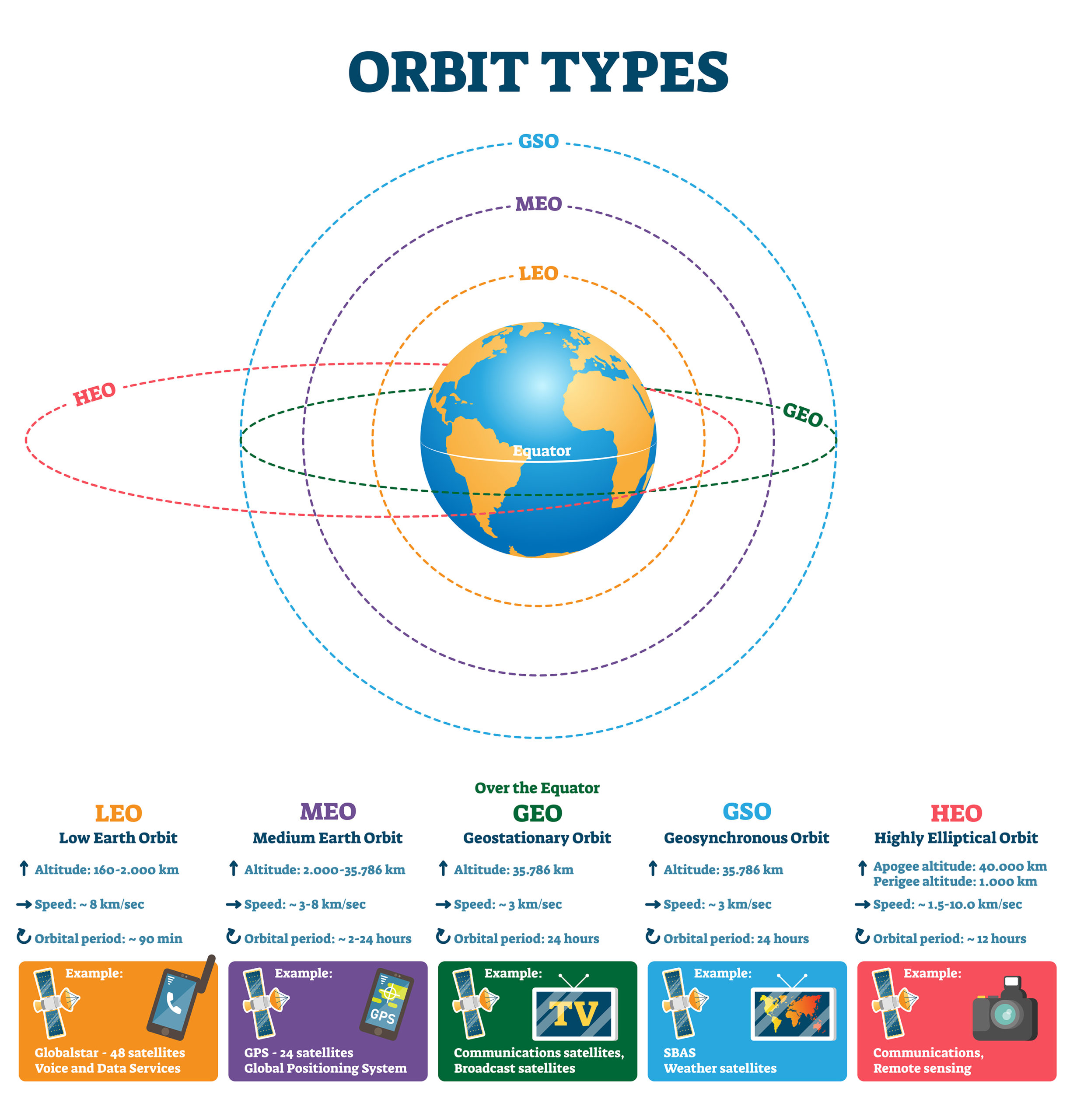 Source: Shutterstock
Source: Shutterstock
2. 3D Geohashes
How can we add altitude (and depth) to geohashes? A theoretically correct approach would be to modify the geohash encoding and decoding algorithms to incorporate altitude directly into the geohash string, making it a true 3D geohash (See postscript below). A simpler approach, used by Geohash-36, is to append altitude data onto the end of the 2D geohash. However, given that we want the ability to use different length geohashes to find nearby events, just using the raw altitude won’t work. We also want the 3D geohash cells to have similar lengths in each dimension (including altitude), and in proportion to the geohash length. The approach we used was to round the altitude value to the same precision as the 2D geohash (which depends on the length) and append it to the 2D geohash with a special character as a separator (e.g. “+”/“-” for altitudes above/below sea level). Note that this approach is only approximate as cubes further away from the earth will be larger than those nearer. The function to round an altitude (a) to a specified precision (p) is as follows:
roundToPrecision(a, p) = round( a / p ) x p
The following table shows the 2D geohash lengths, precision, area and volume for the corresponding 3D geohashes:
| 2D geohash length | precision (m) | precision (km) | area (km^2) | volume (km^3) |
| 1 | 5000000 | 5000 | 25000000 | 1.25E+11 |
| 2 | 1260000 | 1260 | 1587600 | 2000376000 |
| 3 | 156000 | 156 | 24336 | 3796416 |
| 4 | 40000 | 40 | 1600 | 64000 |
| 5 | 4800 | 4.8 | 23.04 | 110.592 |
| 6 | 1220 | 1.22 | 1.4884 | 1.815848 |
| 7 | 152 | 0.152 | 0.023104 | 0.003511808 |
| 8 | 38 | 0.038 | 0.001444 | 0.000054872 |
Note that we refer to the length of the 3D geohash as the base 2D geohash length, even though the 3D geohash is obviously longer due to the appended altitude characters. For an 8 character 2D geohash, the 3D geohash represents a cube with 38m sides. At the other extreme, for 1 character, the cube is a massive 5000km on each side. For a 2 character geohash this is what the approximate 1,000km^3 cube (representing all the world’s water) looks like;
Some example altitudes encoded as a 3D geohash are as follows:
| altitude (m) | 3D geohash | notes |
| 0 | “sv95xs01+0” | Dead sea, sea level |
| -500 | “sv95xs0-494” | Dead sea, below sea level |
| 50 | “sv95xs01+38” | Dead sea, 50m altitude |
| 100 | “sv95xs01+114” | Dead sea, 100m altitude |
| 8848 | “tuvz4+9600” | Mount Everest, cube with 4.8km sides |
| 8848 | “tuvz+0” | Mount Everest, 3D geohash cube with 40km sides |
| 35786000 | “x+35000000” | geostationary satellite orbit, 3D geohash cube with 5,000km sides |
Geostationary satellites appear to be fixed over the same position on the earth, which has to be close to the equator, and because they all have to be 35,786 km up it gets a bit crowded (an average 73km separation). So the above geohash example, “x+35000000”, could “net” around 68 satellites in a cube 5,000km on each side.
Because the 3D geohash is based on latitude/longitude it’s an example of a earth-centered rotational coordinate system, as the coordinates remain fixed on the earth’s surface (i.e. the frame of reference is the earth’s surface, and rotates with it). For objects that are in space, it’s easier to use a Earth-centered inertial coordinate system which doesn’t move with the earth’s rotation, so (for objects further away) their location doesn’t change rapidly.
I was curious about what coordinate systems were used for the Apollo moon landings, now almost exactly 50 years ago.
The answer was “lots”. All the stages of the rocket, including the command/service module and lunar module each used a local coordinate system. This made it easier for the astronauts to compute course correction burns. But there were also many other coordinate systems (the guidance computer translated between them): Earth basic, Moon basic, Earth launch site, passive thermal control (the “barbecue roll”), preferred lunar orbital insertion, lunar landing site, preferred lunar orbital plane change, LM ascent, preferred trans-Earth injection, and Earth entry.
And given that everyone knows the earth is not really the centre of the universe, there are sun centred coordinate systems to (and Galactic and Supergalactic!) This brings us back to full circle to 2D again, as typically distance isn’t relevant for astronomical objects (because it’s unknown or infinite), so stars, black holes, galaxies etc. are assumed to be located on the imaginary celestial sphere (the glass sphere in this antique example): Celestial globe enclosing a terrestrial globe, from 1739 (Source: sciencemuseum.org.uk)
Celestial globe enclosing a terrestrial globe, from 1739 (Source: sciencemuseum.org.uk)
3. Do 3D Geohashes Impact Partition Cardinality?
By using 3D geohashes I realised that we are increasing the cardinality, which may go some of the way to solving the issue we identified at the end of the Blog 2 on Geospatial Anomaly Detection: Geohashes (2D) With shorter geohash partitions being too large. Doing some calculations of the 3D geohash cardinality reveals that the increase in cardinality depends on the altitude range actually in use. For example, if the altitude range is as far as the geostationary satellite orbits, then the cardinality of the 3D geohash based on the 3 character 2D geohash (green) is now high enough to use as the partition key (previously by itself the 4 character 2D geohash was the shortest geohash that would work, orange).
| 2D geohash length | 2D cardinality | 2D cardinality > 100000 | 3D cardinality (0-30,000km altitude) | 3D cardinality > 100000 |
| 1 | 32 | FALSE | 192 | FALSE |
| 2 | 1024 | FALSE | 24576 | FALSE |
| 3 | 32768 | FALSE | 6324224 | TRUE |
| 4 | 1048576 | TRUE | 786432000 | TRUE |
| 5 | 33554432 | TRUE | 2.09715E+11 | TRUE |
| 6 | 1073741824 | TRUE | 2.64044E+13 | TRUE |
| 7 | 34359738368 | TRUE | 6.78155E+15 | TRUE |
| 8 | 1.09951E+12 | TRUE | 8.68036E+17 | TRUE |
However, this is highly sensitive to the subrange of altitudes in use. A 0-100km altitude subrange has no useful impact on the cardinality, but a subrange of 0-400,000km (the approximate distance from the earth to the moon) gives the 3D geohash based on the 2 character 2D geohash high enough cardinality to act as the partition key.
4. A Drone Proximity Anomaly Detection Example
 (Source: Shutterstock)
(Source: Shutterstock)
To test the 3D geohash with the Anomalia Machina pipeline we generated random 3D location data, but rather than shooting for the moon, we limited it to the low-altitudes legally permitted for drones (a few hundred metres high). At these altitudes, the 8 and 7 character geohashes can adequately distinguish locations with nearby altitudes (with a precision of 38m and 152m respectively). This is a realistic simulation of future piloted or automated Drone delivery or monitoring platforms, perhaps working in complex built-up environments, where there are many hazards that drones need to navigate around.
An example of a more concrete drone anomaly detection problem is when the value to be checked is a count of the number of proximity alerts for each drone and location. The proximity alerts could jump if drones started operating near built-up or congested areas, near exclusion zones, or near temporary flight restriction areas. The rules for drone proximity are complex as permitted distances from drones to different types of hazards vary (and vary across the world). Some hazards are likely to be in fixed locations (e.g. airports and built-up areas), others will themselves be moving as will the drones (e.g. vehicles). We’ll focus on fixed hazards only (moving hazards could be processed by Kafka streams and state store application), and assume that proximity is measured in 3D. The rules for fixed hazards (in the UK) are (1) > 50m from people and property (2) > 150m from congested areas (3) > 1000m from airports, and (4) > 5000m (a guess) from emergency exclusion zones (e.g. fires).
 (Source: CASA)
(Source: CASA)
How could we generate proximity alerts for rules like this? Geohashes are again a good fit due to their natural ability to model locations at different scales. A different Cassandra table can be used for each type of hazard, with a 3D geohash as the partition key, where the partition key for each table is chosen to be based on the 2D geohash length closest to the hazard scale. We can simply query each table with the drone location to check if (and how many) hazards of each type are too close to the drone, i.e. geohash8 for people and property (38m precision), geohash7 for congested areas (152m precision), geohash6 for airports (1220m precision), and geohash5 for emergency exclusion zones (4800m precision). The resulting counts would then be fed to the 3D geospatial anomaly detector for checking.
Also note that if we want to increase the precision of the altitude for Drone operations, perhaps to enable altitude to be accurate to within 1m to ensure Drones are hovering outside the correct floor of a skyscraper (e.g. to support emergency services, maintenance, etc), then a 3D geohash constructed from a 10 character 2D geohash, with altitude rounded to 1m appended, can be used (which is a 1 cubic metre box).
Next blog: We investigate using some of the powerful geospatial features of the Lucene Cassandra index plugin, and implement a subset of the alternatives from all the blogs, and run load tests with the Anomalia Machina system. The winner will be revealed in the next blog.
Postscript – Example 3D Geohash code
If you really want to check for drone proximity anomalies correctly, and not cause unnecessary panic in the general public by claiming to have found UFOs instead, then it is possible to use a more theoretically correct 3D version of geohashes. If the original 2D geohash algorithm is directly modified so that all three spatial coordinates (latitude, longitude, altitude), are used to encode a geohash, then geohash ordering is also ensured. Here’s example code in gist for a 3D geohash encoding which produces valid 3D geohashes for altitudes from 13km below sea level to geostationary satellite orbit. Note that it’s just sample code and only implements the encoding method, a complete implementation would also need decoder and other helper functions.
The tradeoff between using the previous “2D geohash+rounded altitude” and this approach is that: (1) this approach is correct, but for the previous approach (2) the 2D part is still compatible with the original 2D geohashes (this 3D geohash is incompatible with it), and (3) the altitude is explicit in the geohash string (it’s encoded into and therefore only implicit in the 3D geohash).
 A 3D Hilbert Cube—the Maths behind geohashes (Source: Claudio Rocchini)
A 3D Hilbert Cube—the Maths behind geohashes (Source: Claudio Rocchini)
Subscribe to our newsletter below or Follow us on LinkedIn or Twitter to get notified when we add the Third Dimension.